How much time usually elapses between two boxes of a comic strip ?
I've been trying to partially answer that question by comparing the comic book "The Seven Crystal Balls" by Hergé with its animated adaptation.

I choose an episode from this particular series because it seemed very close to the book, so it was easy for me to define te precise timing when an event from a box happened or a particular word was pronounced.




There are 784 boxes in the comic book and the film is about 40 minutes long which means a rough estimation would be 3 seconds per box in average.
There are some differences that might biase the results though :
The chronological order of some of the sequences were changed.
The series has some opening and closing credits and an intermission in the middle.
Some dialogs where shortened or extended.
Some parts of the book were entirely removed in the movie (mostly those where Captain Haddock is seen drinking alcohol).
There are some ellipses both in the book and the film (such as "a few days later...") but since I was more intereseted in the continuous time sections I choose to use the actual 'screen-time' values of the animated film instead of making 'world-time' estimations in those cases.
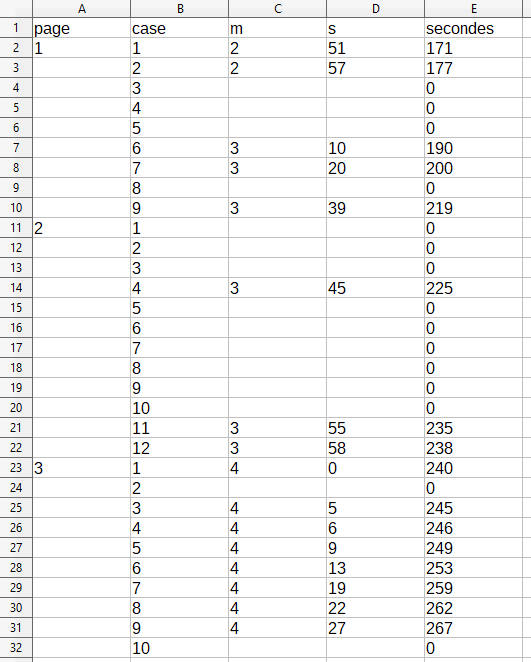
the .ods file
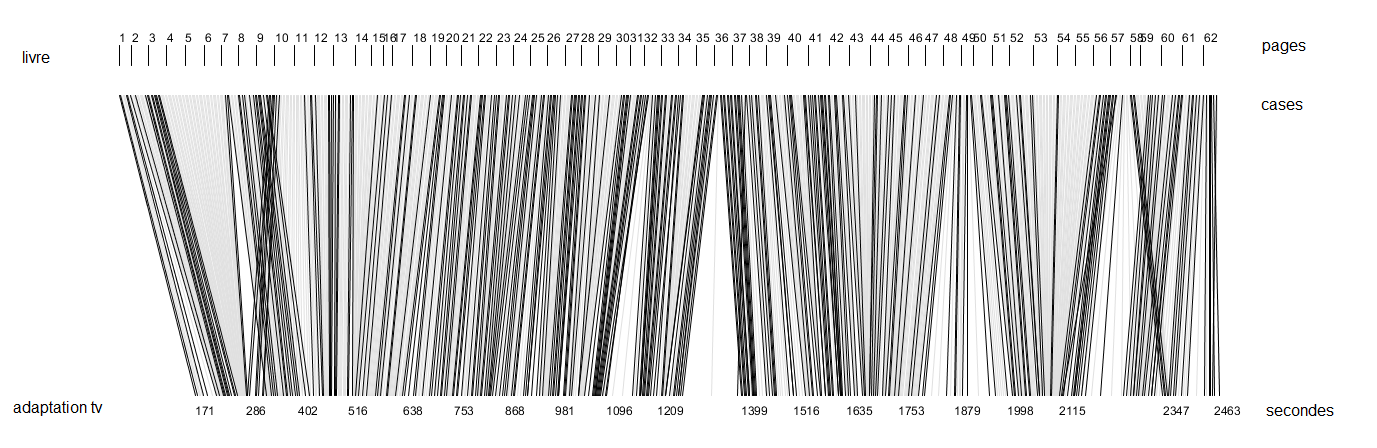
I wrote the timing of every matching point between a box and a frame in a spreadsheet so I could build some graphs out of it (inconsistenly labelled in french and english).
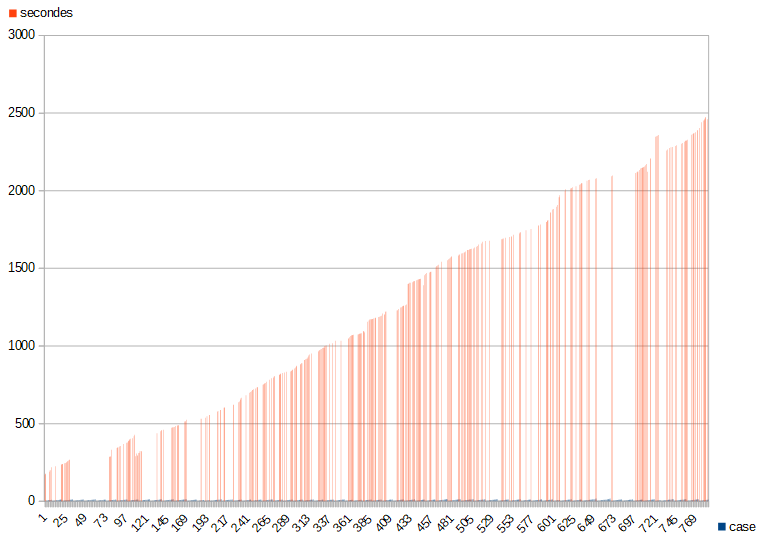
Then I interpolated all the known values in order to assign a timing to each box.
In the graph below black lines represent known values and grey ones represent inferred values.
And here is the distribution of gaps between boxes (merged within 1 second ranges, inferred values in grey).
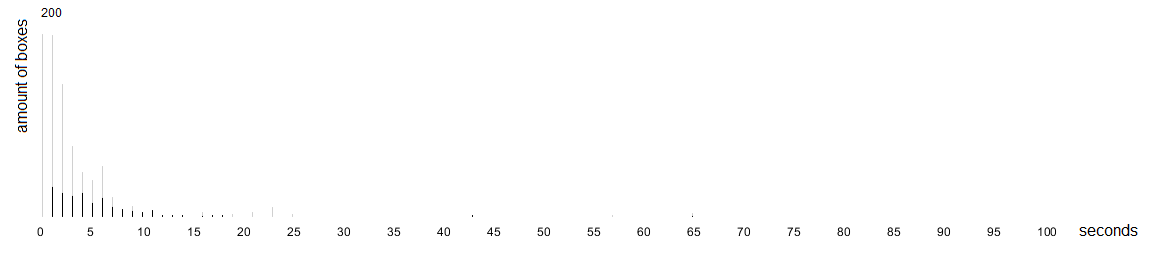
I could find a better average time between two boxes by using some constraints :
- I only considered consecutive boxes with known timings.
- I used times between 0 and 30 seconds (negative or very positive values usually occur when the book and the film differ too much).
The answer is 4.6 seconds.










